Fowler–Noll–Vo hash function

Fowler–Noll–Vo is a non-cryptographic hash function created by Glenn Fowler, Landon Curt Noll, and Phong Vo.

The basis of the FNV hash algorithm was taken from an idea sent as reviewer comments to the IEEE POSIX P1003.2 committee by Glenn Fowler and Phong Vo back in 1991. In a subsequent ballot round, Landon Curt Noll improved on their algorithm. Some people tried this hash and found that it worked rather well. In an EMail message to Landon, they named it the ``Fowler/Noll/Vo or FNV hash. ^[1]

1 Overview
2 The hash
- 2.1 FNV-1 hash
- 2.2 FNV-1a hash
3 See also
4 Notes
5 External links

Overview

The current versions are FNV-1 and FNV-1a, which supply a means of creating non-zero FNV offset basis. FNV currently comes in 32-, 64-, 128-, 256-, 512-, and 1024-bit flavors. For pure FNV implementations, this is determined solely by the availability of FNV primes for the desired bit length; however, the FNV webpage discusses methods of adapting one of the above versions to a smaller length that may or may not be a power of two. ^[2]^[3]

The FNV hash algorithms and sample FNV source code have been released into the public domain. ^[4]

FNV is not a cryptographic hash.

The hash

One of FNV's key advantages is that it is very simple to implement. Start with an initial hash value of FNV offset basis. For each byte in the input, multiply hash by the FNV prime, then XOR it with the byte from the input. The alternate algorithm, FNV-1a, reverses the multiply and XOR steps.

FNV-1 hash

The FNV-1 hash algorithm is as follows: ^[5]

   hash = FNV_offset_basis
   for each octet_of_data to be hashed
   	hash = hash  FNV_prime
   	hash = hash XOR octet_of_data
   return hash

In the above pseudocode, all variables are unsigned integers. All variables, except for octet_of_data, have the same number of bits as the FNV hash. The variable, octet_of_data, is an 8 bit unsigned integer.

As an example, consider the 64-bit FNV-1 hash:

All variables, except for octet_of_data, are 64-bit unsigned integers.
The variable, octet_of_data, is an 8 bit unsigned integer.
The FNV_offset_basis is the 64-bit FNV offset basis value: 14695981039346656037.
The FNV_prime is the 64-bit FNV prime value: 1099511628211.
The multiply (indicated by the 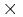$\times$ symbol) returns the lower 64-bits of the product.
The XOR is an 8-bit operation that modifies only the lower 8-bits of the hash value.
The hash value returned is an 64-bit unsigned integer.

The values for FNV prime and FNV offset basis may be found in this table.^[6]

FNV-1a hash

The FNV-1a hash differs from the FNV-1 hash by only the order in which the multiply and XOR is performed: ^[7]

   hash = FNV_offset_basis
   for each octet_of_data to be hashed
   	hash = hash XOR octet_of_data
   	hash = hash  FNV_prime
   return hash

The above pseudocode has the same assumptions that were noted for the FNV-1 pseudocode. The small change in order leads to much better avalanche characteristics. ^[8]

Notes

External links

Landon Curt Noll's webpage on FNV (with table of base & prime parameters)
Internet draft by Fowler, Noll, Vo, and Eastlake (2011, work in progress)